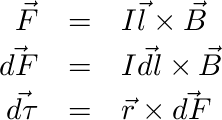
As the coils generate an opposing magnetic field there will be force on the coils pushing them apart. We try to calculate this force against an individual coil. We use the Lorentz force equation on a wire segment. This can also be used to calculate the torque on a coil (in case of misalignments). We treat the coil as a ring of current. The math looks like this:
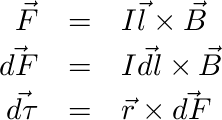
We can numerically integrate over a coil calculating individual force and torque elements, summing them up. The r vector is a vector from the center of the coil to the given point (as the coil is symmetric). Also as the same current I is present also in the B vector we can generalize the equation against 1 ampere force k as F=k*I^2. In case the coils are perfectly aligned the force is perpendicular to the measured coil plane pointing away and the torque is zero.
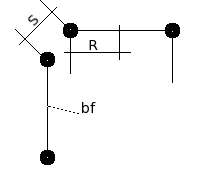Lets sample some configurations.
| RADIUS(R)[m] | SPACING(S)[m] | k(F=k*I^2) | F(I=10000A)[N] | F(I=50000A)[N] | F(I=100000A)[N] |
| 0.15 | 0.08 | 9.24698e-07 | 92 | 2312 | 9246 |
| 0.3 | 0.1 | 1.57079e-06 | 157 | 3927 | 15707 |
| 1.0 | 0.2 | 2.53945e-06 | 254 | 6349 | 25395 |
What about torque. Lets take an example when the measured coil is misaligned by 5 degrees (around its center).
The torque comes at some 22Nm but also note there is significant lateral force.radius = 0.150000 m spacing = 0.080000 m current = 50000.000000 A offset = 5.000000 degrees normal = (0.0871557, 0, -0.996195) F = (228.179, -6.08301e-13, 2273.5) T = (-1.39748e-14, -21.6537, -3.13878e-15)
The mechanical engineering problems probably come down to making sure adequate damping is in place and no resonances come up as the system might easily shake itself apart in that case.