Cube polywell symmetries

When doing calculations on polywell it makes sense to pay attention to inherent symmetries in the system. The fields in 3D are unique in only so many places. For example when storing a 3D grid of data symmetries can help to save memory. Also many calculation methods can be simplified and sped up if the number of elements in the calculations is reduced.

The very first obvious thing to do would be to divide the cube polywell into 8 different pieces. This reduces the amount of data for same resolution in a 3D grid by 1/8.

This animated gif helps to show where the 1/8 is picked out:

When looking closely at this image you can see that there is a symmetry. One can split the cube vertically and get a triangular prism:

This reduces the amount of data in a 3D grid by 1/16 of the original. The truth is that starting from here this kind of division is complicated to use in a uniform grid as all grid sides are not the same and so memory management, indexing and finding grid values is complicated. But it works pefectly out for one other space partitioning algorithm: 3D octree grid.

Lets try another animated gif:

There is a not so obvious symmetry involved here. One can cut away 2/3 of the triangular prism.

This reduces the amount of 3D grid data to 1/48 of the original:

We've been chucking stuff off the cube polywell. This is how we did it:

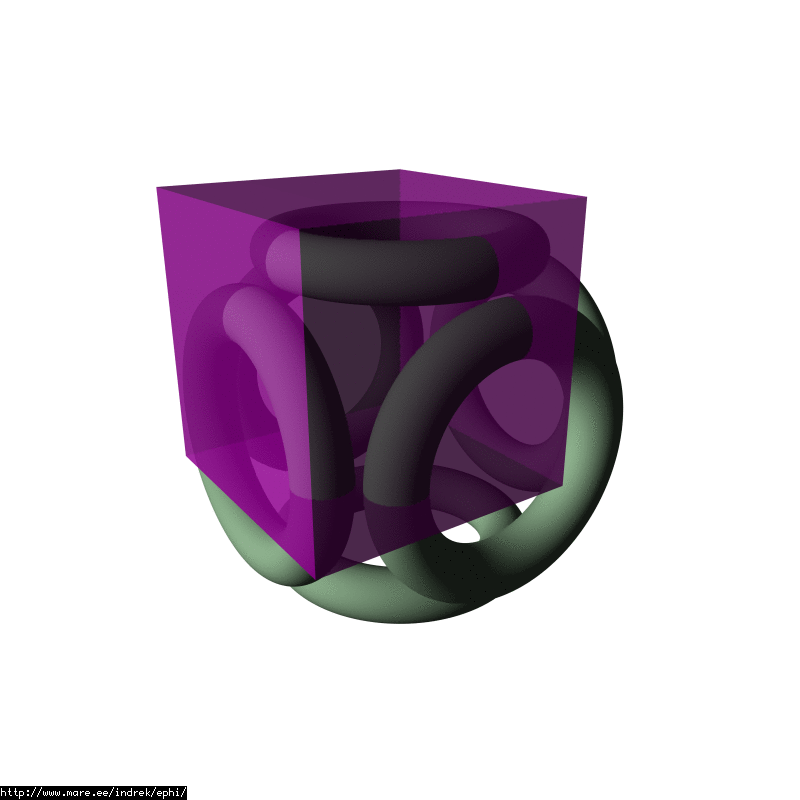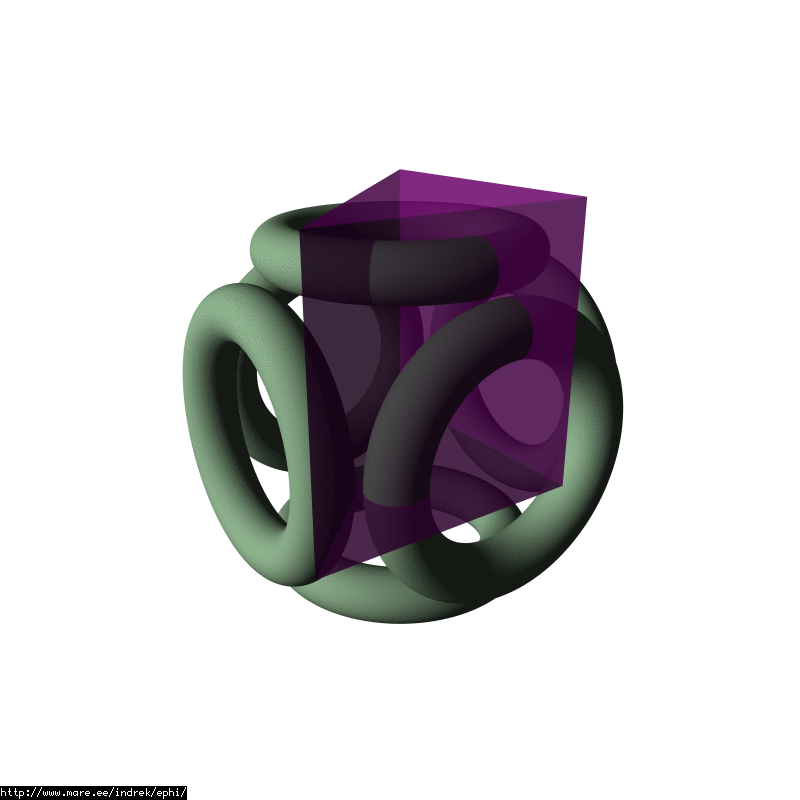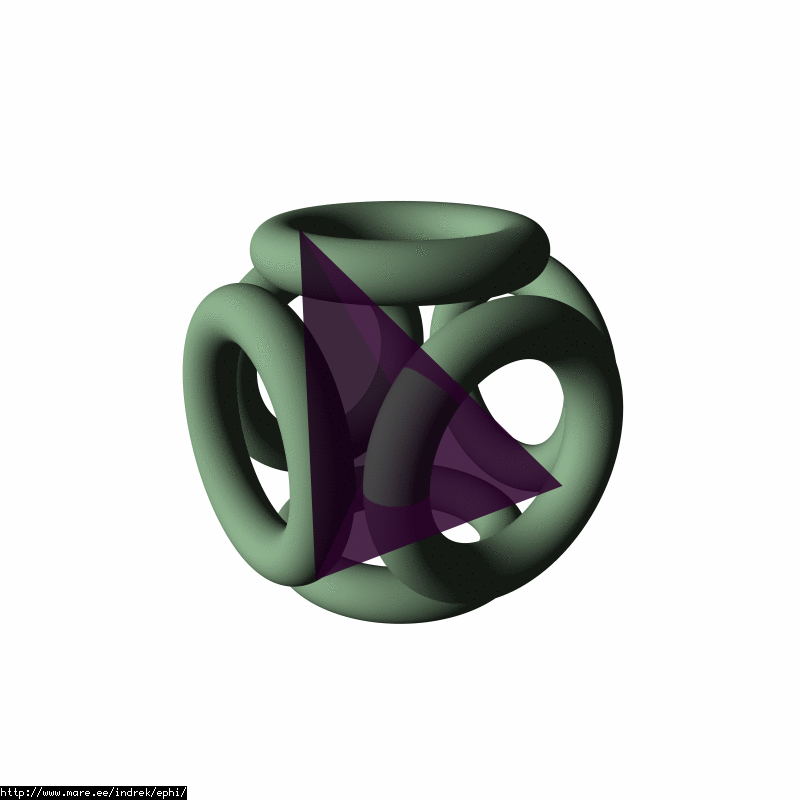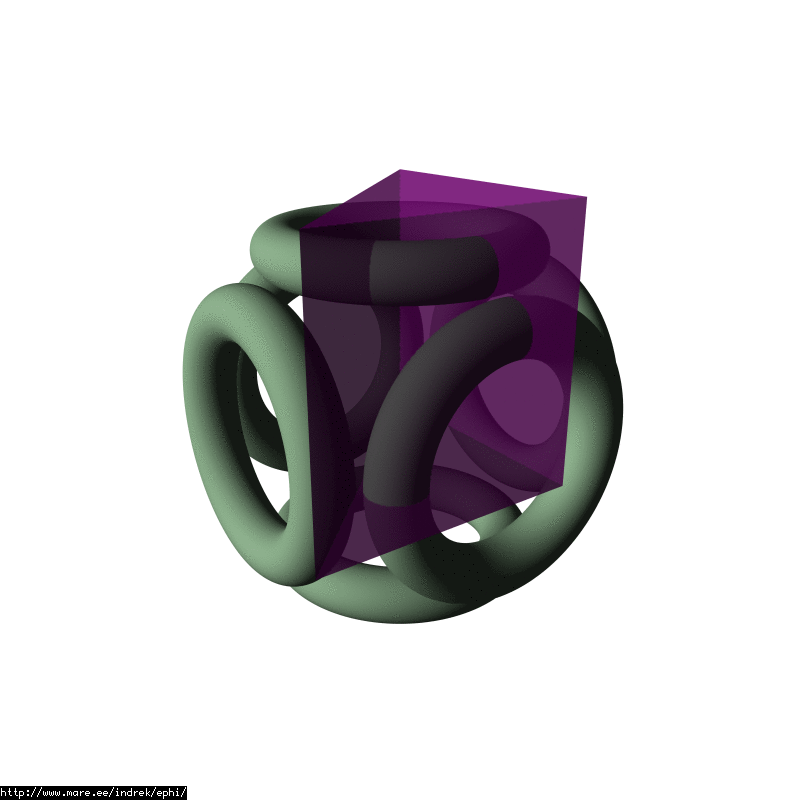
Now when one would want to look up a field value (a vector) at a specific point using the grid then the algorithm would be to first project the point to the positive sides of symmetry planes one at a time, finally getting the field value at our limited space of the grid. Now this value has to be reversed - for that one would just have to apply the plane projections in reverse to the field vector value (one can simply treat the vector value itself as a point against the planes).

One set of the five plane normal vectors dividing this 1/48 of space would be:

(1, 0, 0)

(0, 1, 0)

(0, 0, 1)

(1, 0, -1)

(0, -1, 1)

One can look at this also as splitting space with 9 intersecting planes:

Return to ephi..