When simulating cube polywell and calculating fields from moving particles, it might make sense to look at inherent symmetries in the system. Specifically we might simulate a particle path in the system but later at field calculations replicate this path according to inherent symmetries.
Coil fields in the cube polywell can be calculated only for 1/48 part as looked in our previous research. Unfortunately this 1/48 splitting cannot be simply used with particle paths. The problem is that the force on a moving particle in a magnetic field is defined as F=qv×B, but this force vector does not translate properly in the diagonal mirrors on the faces:

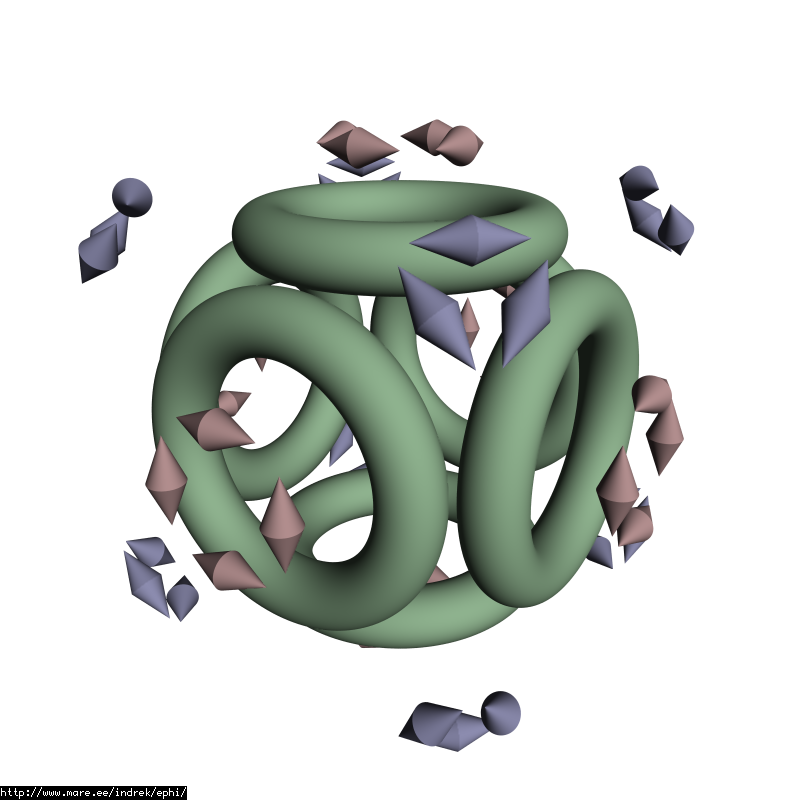
The charged particle will only move one way around the field lines. Thus we have to drop half the symmetry and only use 1/24:

This 1/24 region will look like this:

As animated gif:

And as sectors divided:

Animated gif:

So when calculating electron paths and fields from that we can mirror them and increase our sample by 24 fold. So from here:

To here:

It turns out the fields from these particles also have to only be calcualted for 1/24th of the system - they can be symmetrically mapped to all other sectors.
Now having said all of this about 1/24. We might consider a trick to get back to 1/48 - reverse the charge of the moving particle when we mirror it diagonally. This will "fix" the force vector and will give us more symmetry at the calculated b-field. Alternatively one can reverse the speed vector to get proper force and b-field out of it and keep the e-field calculations correct.
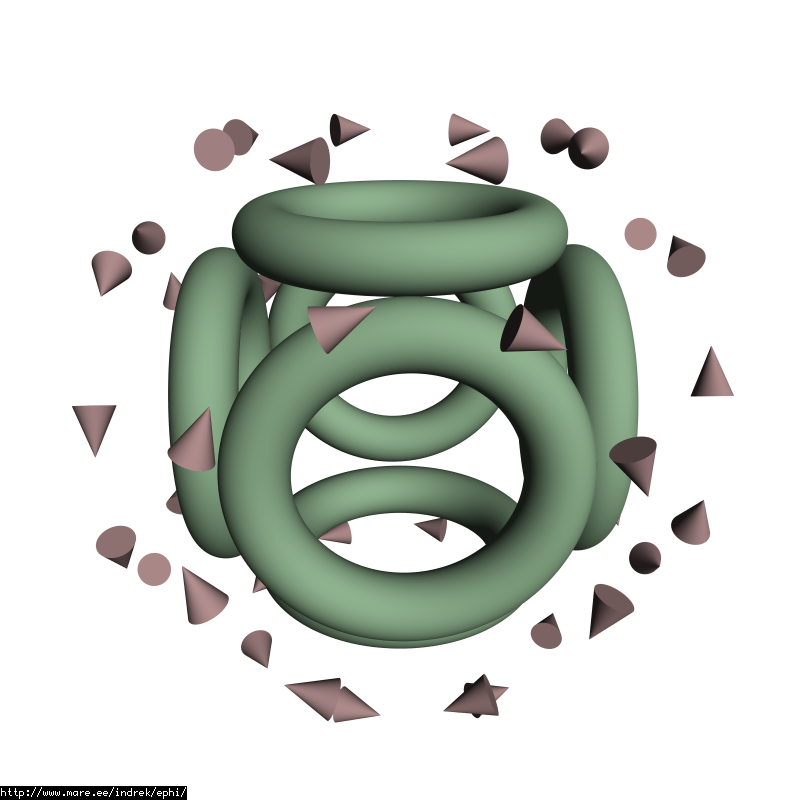
And an animated gif how a single point would be mapped into 48 different ones with speed/direction reversed:

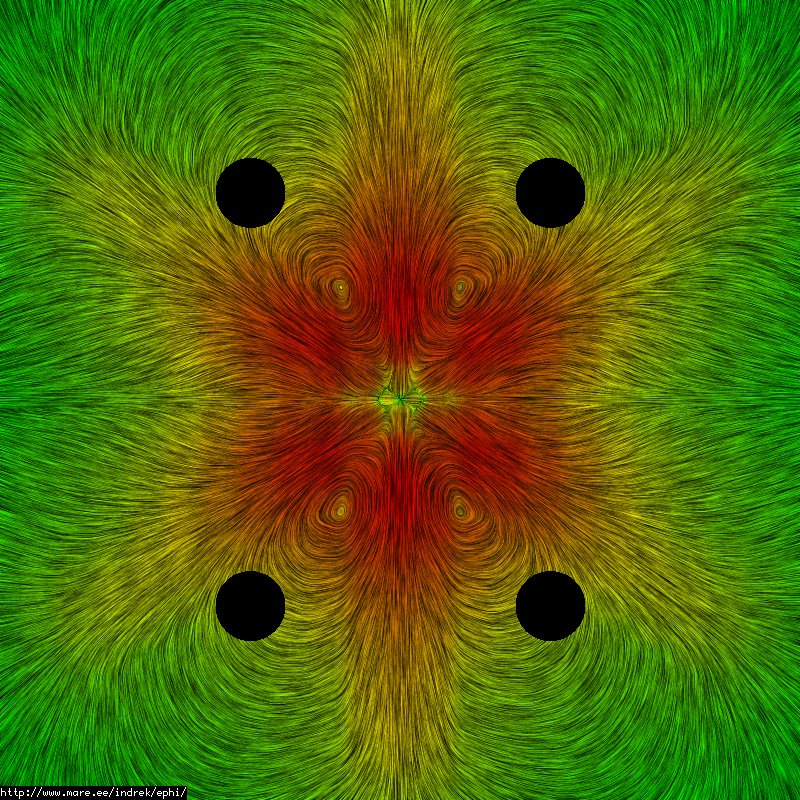
Preliminary tests seem to indicate that reversing the speed vector works fine and results in fields that are completely symmetric. Here's an approximation of the diamagnetic field generated by the electrons opposing the coil fields:
Copyright © 2007 Indrek Mandre