|
libfbm
0.3
Simulation of multi-dimensional stationary Gaussian processes and fractional Brownian motion.
|
|
libfbm
0.3
Simulation of multi-dimensional stationary Gaussian processes and fractional Brownian motion.
|
This library generates (simulates) multi-dimensional random fields:
Stationary means here that the covariance between two points does not depend on the individual coordinates of the points:
![\[ \mbox{Cov}\!\left(Z\!\left(\mathbf{x}\right),Z\!\left(\mathbf{y}\right)\right)\equiv\rho\!\left(\mathbf{x}-\mathbf{y}\right), \]](form_0.png)
so that only the vector 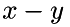 is used. Gaussian means that the distribution of individual values in the field is gaussian and the process can be completely described by its mean and covariance matrix, that is when
is used. Gaussian means that the distribution of individual values in the field is gaussian and the process can be completely described by its mean and covariance matrix, that is when
![\[ \left[Z\!\left(\mathbf{x}_{1}\right),\ldots,Z\!\left(\mathbf{x}_{m}\right)\right]^{T}\sim\mathcal{N}\!\left(\boldsymbol{\mu},\boldsymbol{\Sigma}\right) \]](form_2.png)
We say the SGP is isotropic, if the covariance depends only on the distance between the two points, that is
![\[ \mbox{Cov}\!\left(Z\!\left(\mathbf{x}\right),Z\!\left(\mathbf{y}\right)\right)\equiv\rho\!\left(\left|\mathbf{x}-\mathbf{y}\right|\right). \]](form_3.png)
We say the SGP is even, if the covariance function has the same value in case of reflection in one dimension, that is when:
![\[ \mbox{Cov}\!\left(Z\!\left(\mathbf{x}\right),Z\!\left(\mathbf{y}\right)\right)\equiv\rho\!\left(\left|x_1-y_1\right|,\ldots,\left|x_d-y_d\right|\right). \]](form_4.png)
Library supports arbitrary-dimensional generation, that is 1D, 2D, 3D, 4D, etc. However, there is a hardcoded limit of 8 (can be changed at library compile time).
For a random engine the library makes use of SFMT [8]. Normal distribution is achieved with an efficient ziggurat algorithm (rejection sampling). Emphasis of the library is on fast bulk-generation of random fields.
With the help of some post-processing also fractional Brownian motion or surfaces (or higher-dimensional fields) can be generated. For the one-dimensional (1D) case this can be done simply by generating the increment process (fractional Gaussian noise), and summing elements to get the fBm itself. For higher-dimensional cases a more involved process is used by Stein [3]. Note that Stein's definition of fBm is different compared to the traditional (strict mathematical) definition – fields generated with his methods also adhere to this change.
Calculation of a SGP involves two N-dimensional fast Fourier transforms. One of them is pre-calculated and can be cached on the hard disk to save memory. For this reason the first invocation of generate() on a given field object may be at least twice as slow as the following calls (unless already cached on HD). The library is meant to be used in Monte Carlo simulations where thousands or millions of field instances are required.
The first Fourier transform results in eigenvalues. For the algorithm to work these must be positive. Sometimes, due to numeric errors or the nature of cov() (the embedded covariance matrix is not positive semi-definite), they can come out negative. When this happens the library complains to stderr. Here are some hints on how to overcome this:
The used methods in this library are derived from [1], [2] and [3]. Also [5] contains useful information and implementation for matlab/octave. Note that these methods are mathematically "exact". That is they are not approximations. Still I should add that here by default we use a pseudo-random random number generataror, which is not "exact". And there are numeric errors that may creep up whenever calculations approach zero or infinity.
The library depends on the FFTW3 library for FFT functions. You can get it from http://www.fftw.org/ but most Linux distribution have a native package for easy installation.
The library requires that the underlyinf architecture uses IEEE 754 format double precision floating point numbers.
I haven't really tested the library that much for non-isotropic or un-even covariance functions. Hopefully, it works properly. If you run into trouble you can use SGPTester to test that the generated process has the expected covariances.
References:
[1] Wood, A. T. A. and Chan, G.
Simulation of Stationary Gaussian Processes in [0, 1]^d.
Journal of Computational and Graphical Statistics, 3(4), 409–432 (1994).
doi:10.1080/10618600.1994.10474655
[2] Dietrich, C. R. and Newsam, G. N.
Fast and Exact Simulation of Stationary Gaussian Processes through
Circulant Embedding of the Covariance Matrix.
SIAM Journal on Scientific Computing, 18(4), 1088–1107 (1997).
doi:10.1137/S1064827592240555
[3] Stein, M. L.
Fast and Exact Simulation of Fractional Brownian Surfaces.
Journal of Computational and Graphical Statistics, 11(3), 587–599 (2002).
doi:10.1198/106186002466
[4] Qian, H., Raymond, G. M. and Bassingthwaighte, J. B.
On two-dimensional fractional Brownian motion and fractional Brownian random field.
J. Phys. A: Math. Gen., 31, L527–L535 (1998).
doi:10.1088/0305-4470/31/28/002
[5] Kroese, D. P. and Botev, I. Z.
Spatial Process Generation.
http://www.maths.uq.edu.au/~kroese/ps/MCSpatial.pdf
[6] Timmer, J. and König, M.
On generating power law noise.
Astronomy and Astrophysics 300: 707 (1995).
[7] Marsaglia, G. and Tsang, W. W.
The Ziggurat Method for Generating Random Variables.
Journal of Statistical Software, 5(8), 1-7 (2000).
[8] Saito, M. and Matsumoto, M.
SIMD-Oriented Fast Mersenne Twister: a 128-bit Pseudorandom Number Generator
Monte Carlo and Quasi-Monte Carlo Methods 2006, Springer, 607-622 (2008).
doi:10.1007/978-3-540-85912-3_26
Example of generating 1D fractional Brownian motion:
Example of generating 2D fractional Brownian surfaces:
Example of generating 2D random process with custom covariance function:
And here's some legalese, the copyright notice for libfbm:
Copyright (c) 2013, Indrek Mandre <indrek(at)mare.ee> All rights reserved.
Redistribution and use in source and binary forms, with or without modification, are permitted provided that the following conditions are met:
a Redistributions of source code must retain the above copyright notice, this list of conditions and the following disclaimer. b Redistributions in binary form must reproduce the above copyright notice, this list of conditions and the following disclaimer in the documentation and/or other materials provided with the distribution.
THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDERS AND CONTRIBUTORS "AS IS" AND ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT LIMITED TO, THE IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE ARE DISCLAIMED. IN NO EVENT SHALL THE COPYRIGHT OWNER OR CONTRIBUTORS BE LIABLE FOR ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL, EXEMPLARY, OR CONSEQUENTIAL DAMAGES (INCLUDING, BUT NOT LIMITED TO, PROCUREMENT OF SUBSTITUTE GOODS OR SERVICES; LOSS OF USE, DATA, OR PROFITS; OR BUSINESS INTERRUPTION) HOWEVER CAUSED AND ON ANY THEORY OF LIABILITY, WHETHER IN CONTRACT, STRICT LIABILITY, OR TORT (INCLUDING NEGLIGENCE OR OTHERWISE) ARISING IN ANY WAY OUT OF THE USE OF THIS SOFTWARE, EVEN IF ADVISED OF THE POSSIBILITY OF SUCH DAMAGE.
Note that this software also uses FFTW, which is under the GPL. It should be trivial to make changes to use a different FFT stack.
Now despite the claims before, this software is not actually free. In case you used it in research resulting in a published paper, or a thesis you defended, you must send me a book. One book per paper. Any book will do. It can be used. I do personally enjoy fiction.
Take care and have fun!!
Indrek Mandre - indrek(at)mare.ee - Institute of Cybernetics at the Tallinn University of Technology - Akadeemia tee 21, 12618, Tallinn, Estonia, EU
This library incorporates SFMT, with the following license:
Copyright (c) 2006,2007 Mutsuo Saito, Makoto Matsumoto and Hiroshima University. Copyright (c) 2012 Mutsuo Saito, Makoto Matsumoto, Hiroshima University and The University of Tokyo. All rights reserved.
Redistribution and use in source and binary forms, with or without modification, are permitted provided that the following conditions are met:
a Redistributions of source code must retain the above copyright
notice, this list of conditions and the following disclaimer.
b Redistributions in binary form must reproduce the above
copyright notice, this list of conditions and the following
disclaimer in the documentation and/or other materials provided
with the distribution.
c Neither the names of Hiroshima University, The University of
Tokyo nor the names of its contributors may be used to endorse
or promote products derived from this software without specific
prior written permission.THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDERS AND CONTRIBUTORS "AS IS" AND ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT LIMITED TO, THE IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE ARE DISCLAIMED. IN NO EVENT SHALL THE COPYRIGHT OWNER OR CONTRIBUTORS BE LIABLE FOR ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL, EXEMPLARY, OR CONSEQUENTIAL DAMAGES (INCLUDING, BUT NOT LIMITED TO, PROCUREMENT OF SUBSTITUTE GOODS OR SERVICES; LOSS OF USE, DATA, OR PROFITS; OR BUSINESS INTERRUPTION) HOWEVER CAUSED AND ON ANY THEORY OF LIABILITY, WHETHER IN CONTRACT, STRICT LIABILITY, OR TORT (INCLUDING NEGLIGENCE OR OTHERWISE) ARISING IN ANY WAY OUT OF THE USE OF THIS SOFTWARE, EVEN IF ADVISED OF THE POSSIBILITY OF SUCH DAMAGE.
Note that the authors of SFMT have nothing to do with libfbm.
TODO:
 1.8.1
1.8.1